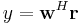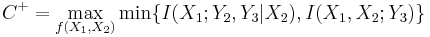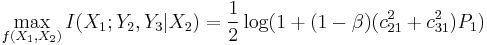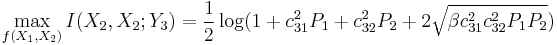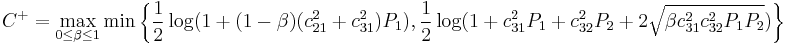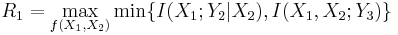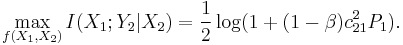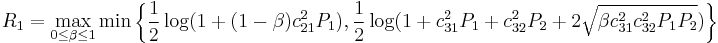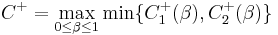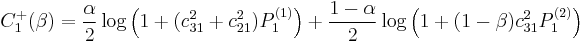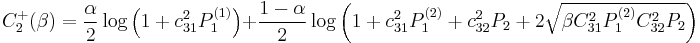Cooperative diversity
Cooperative diversity is a cooperative multiple antenna technique for improving or maximising total network channel capacities for any given set of bandwidths which exploits user diversity by decoding the combined signal of the relayed signal and the direct signal in wireless multihop networks. A conventional single hop system uses direct transmission where a receiver decodes the information only based on the direct signal while regarding the relayed signal as interference, whereas the cooperative diversity considers the other signal as contribution. That is, cooperative diversity decodes the information from the combination of two signals. Hence, it can be seen that cooperative diversity is an antenna diversity that uses distributed antennas belonging to each node in a wireless network. Note that user cooperation is another definition of cooperative diversity. User cooperation considers an additional fact that each user relays the other user's signal while cooperative diversity can be also achieved by multi-hop relay networking systems.
Contents |
Relaying Strategies
Cooperative diversity can be performed based on a few different relaying strategies such as amplify-and-forward, decode-and-forward, and compress-and-forward strategies.
- The amplify-and-forward strategy allows the relay station to amplify the received signal from the source node and to forward it to the destination station
- The decode-and-forward strategy allows the relay station to decode the received signal from the source node, re-encode it and forward it to the destination station
- The compress-and-forward strategy allows the relay station to compress the received signal from the source node and forward it to the destination without decoding the signal where Wyner-Ziv coding can be used for optimal compression.
Relay Transmission Topology
Serial Relay Transmission
Serial relay transmission is used for long distance communication and range-extension in shadowy region. It provides power gain. In this topology signal propagate from one relay to another relay and the channels of neighboring hop are orthogonal to avoid any interference.
Parallel Relay Transmission
The serial relay transmission suffers from multi-path fading. For outdoors and non-line of sight communication, signal wavelength may be large and installation of multiple antennas are not possible. To increase the robustness against multi-path fading, parallel relay transmission can be used. In this topology, signal propagate through multiple relay path in same hop and destination combine the signals received with the help of various combining schemes. It provides power gain and diversity gain simultaneously.
System model
We consider a wireless relay system that consists of source, relay and destination nodes. It is assumed that the channel is in a half-duplex, orthogonal and amplify-and-forward relaying mode. Differently to the conventional direct transmission system, we exploit a time division relaying function where this system can deliver information with two temporal phases.
On the first phase, the source node broadcasts information 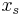 toward both the destination and the relay nodes. The received signal at the destination and the relay nodes are respectively written as:
toward both the destination and the relay nodes. The received signal at the destination and the relay nodes are respectively written as:
where 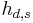 is the channel from the source to the destination nodes,
is the channel from the source to the destination nodes, 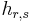 is the channel from the source to the relay node,
is the channel from the source to the relay node, 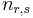 is the noise signal added to
is the noise signal added to 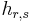 and
and 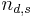 is the noise signal added to
is the noise signal added to 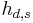 .
.
On the second phase, the relay can transmit its received signal to the destination node except the direct transmission mode.
Signal Decoding
We introduce four schemes to decode the signal at the destination node which are the direct scheme, the non-cooperative scheme, the cooperative scheme and the adaptive scheme. Except the direct scheme, the destination node uses the relayed signal in all other schemes.
Direct Scheme
In the direct scheme, the destination decodes the data using the signal received from the source node on the first phase where the second phase transmission is omitted so that the relay node is not involved in transmission. The decoding signal received from the source node is written as:
While the advantage of the direct scheme is its simplicity in terms of the decoding processing, the received signal power can be severely low if the distance between the source node and the destination node is large. Thus, in the following we consider non-cooperative scheme which exploits signal relaying to improve the signal quality.
Non-cooperative Scheme
In the non-cooperative scheme, the destination decodes the data using the signal received from the relay on the second phase, which results in the signal power boosting gain. The signal received from the relay node which retransmits the signal received from the source node is written as:
where 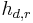 is the channel from the relay to the destination nodes and
is the channel from the relay to the destination nodes and 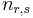 is the noise signal added to
is the noise signal added to 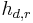 .
.
The reliability of decoding can be low since the degree of freedom is not increased by signal relaying. There is no increase in the diversity order since this scheme exploits only the relayed signal and the direct signal from the source node is either not available or is not accounted for. When we can take advantage of such a signal and increase in diversity order results. Thus, in the following we consider the cooperative scheme which decodes the combined signal of both the direct and relayed signals.
Cooperative Scheme
For cooperative decoding, the destination node combines two signals received from the source and the relay nodes which results in the diversity advantage. The whole received signal vector at the destination node can be modeled as:
where 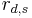 and
and 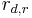 are the signals received at the destination node from the source and relay nodes, respectively. As a linear decoding technique, the destination combines elements of the received signal vector as follows:
are the signals received at the destination node from the source and relay nodes, respectively. As a linear decoding technique, the destination combines elements of the received signal vector as follows:
where 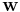 is the linear combining weight which can be obtained to maximize signal-to-noise ratio (SNR) of the combined signals subject to given the complexity level of the weight calculation.
is the linear combining weight which can be obtained to maximize signal-to-noise ratio (SNR) of the combined signals subject to given the complexity level of the weight calculation.
Adaptive Scheme
Adaptive scheme selects one of the three modes described above which are the direct, the non-cooperative, and the cooperative schemes relying on the network channel channel state information and other network parameters.
Trade-off
It is noteworthy that cooperative diversity can increase the diversity gain at the cost of losing the wireless resource such as frequency, time and power resources for the relaying phase. Wireless resources are wasted since the relay node uses wireless resources to relay the signal from the source to the destination node. Hence, it is important to remark that there is trade-off between the diversity gain and the waste of the spectrum resource in cooperative diversity.
Channel Capacity of Cooperative Diversity
In June 2005, A. Høst-Madsen published a paper in-depth analyzing the channel capacity of the cooperative relay network.[1]
We assume that the channel from the source node to the relay node, from the source node to the destination node, and from the relay node to the destination node are 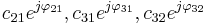 where the source node, the relay node, and the destination node are denoted node 1, node 2, and node 3, subsequently.
where the source node, the relay node, and the destination node are denoted node 1, node 2, and node 3, subsequently.
The capacity of cooperative relay channels
Using the max-flow min-cut theorem yields the upper bound of full duplex relaying
where 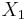 and
and 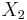 are transmit information at the source node and the relay node respectively and
are transmit information at the source node and the relay node respectively and  and
and 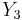 are received information at the relay node and the destination node respectively. Note that the max-flow min-cut theorem states that the maximum amount of flow is equal to the capacity of a minimum cut, i.e., dictated by its bottleneck. The capacity of the broadcast channel from
are received information at the relay node and the destination node respectively. Note that the max-flow min-cut theorem states that the maximum amount of flow is equal to the capacity of a minimum cut, i.e., dictated by its bottleneck. The capacity of the broadcast channel from 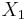 to
to  and
and 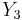 with given
with given 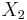 is
is
while the capacity of the multiple access channel from 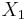 and
and 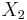 to
to 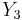 is
is
where  is the amount of correlation between
is the amount of correlation between 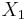 and
and 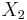 . Note that
. Note that 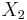 copies some part of
copies some part of 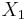 for cooperative relaying capability. Using cooperative relaying capability at the relay node improves the performance of reception at the destination node. Thus, the upper bound is rewritten as
for cooperative relaying capability. Using cooperative relaying capability at the relay node improves the performance of reception at the destination node. Thus, the upper bound is rewritten as
Achievable rate of a decode-and-forward relay
Using a relay which decodes and forwards its captured signal yields the achievable rate as follows:
where the broadcast channel is reduced to the point-to-point channel because of decoding at the relay node, i.e., 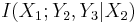 is reduced to
is reduced to 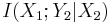 . The capacity of the reduced broadcast channel is
. The capacity of the reduced broadcast channel is
Thus, the achievable rate is rewritten as
Time-Division Relaying
The capacity of the TD relay channel is upper-bounded by
with
Applications
Cooperative sensing for cognitive radio
In cognitive radio system, unlicensed secondary users can use the resources which is licensed for primary users. When primary users want to use their licensed resources, secondary users has to vacant these resources. Hence secondary users has to constantly sense the channel for detecting the presence of primary user. It is very challenging to sense the activity of spatially distributed primary users in wireless channel. Spatially distributed nodes can improve the channel sensing reliability by sharing the information and reduce the probability of false alarming.
Wireless Ad-hoc network
This is autonomous and self organizing network without any centralized controller or pre-established infrastructure. In this network randomly distributed nodes forms a temporary functional network and support seamless leaving or joining of nodes. Such network has been successfully deployed for military communication and have lot of potential for civilian applications include commercial and educational use, disaster management, road vehicle network etc.
Wireless sensor network
Cooperative relaying can be used to reduce the energy consumption in sensor nodes, hence lifetime of sensor network increases. Due to nature of wireless medium, communication through weaker channels requires huge energy as compared to relatively stronger channels. Careful incorporation of relay cooperation into routing process can selects better communication links and precious battery power can be saved.
References
- ^ A. Høst-Madsen and J. Zhang (June, 2005). "Capacity bounds and power allocation for the wireless relay channel". IEEE Trans. Inform. Theory 51 (6): 2020–2040. doi:10.1109/TIT.2005.847703. http://www.it.iitb.ac.in/~subbu/pdf_ps/relay_channel1.pdf.
See also
Systems
- 3GPP long term evolution (LTE) coordinated multipoint transmission/reception (CoMP), making it possible to increase the data rate to and from a mobile situated in the overlap of several base stations.
- 5G
- Mesh network
- Mobile ad-hoc network (MANet)
- Wireless mesh network
- Wireless ad-hoc network
Technologies
- Cooperative wireless communications
- Cooperative MIMO
- Diversity schemes
- Dynamic Single Frequency Networks (DSFN)
- Soft handover
- Space–time code
- Multiple-input multiple-output communications (MIMO)
- Multi-user MIMO
- Diversity combining
- Transmit diversity
- Diversity gain
External references
- A. Sendonaris, E. Erkip, and B. Aazhang, “User Cooperation Diversity Part I and Part II,” IEEE Trans. Commun., vol. 51, no. 11, November 2003, pp. 1927–48.
- J. N. Laneman, D. N. C. Tse, and G. W. Wornell, “Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behavior,” IEEE Trans. Inform. Theory, vol. 50, no. 12, pp. 3062–3080, December 2004.
- S. Valentin, et al., Cooperative wireless networking beyond store-and-forward: Perspectives for PHY and MAC design
- Sébastien Simoens, Josep Vidal, Olga Muñoz, COMPRESS-AND-FORWARD COOPERATIVE RELAYING IN MIMO-OFDM SYSTEMS
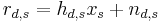
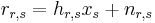
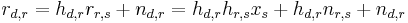
![\mathbf{r} = [r_{d,s} \quad r_{d,r}]^T
= [h_{d,s} \quad h_{d,r} h_{r,s}]^T x_{s} %2B \left[1 \quad \sqrt{|h_{d,r}|^2%2B1} \right]^T n_{d}
= \mathbf{h} x_{s} %2B \mathbf{q} n_{d}](/2012-wikipedia_en_all_nopic_01_2012/I/756fda848b1765f90dd370da61873720.png)